Тип задания:
Геометрия. №25.
Сторона AB параллелограмма ABCD вдвое больше стороны AD. Точка K — середина стороны AB. Докажите, что DK — биссектриса угла ADC.
Решение:
Соединим точки D и K.
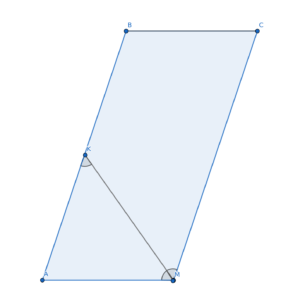
По условию, K-середина AB и AB=2\cdot AD . Следовательно, AK=AD. Тогда треугольник DAK — равнобедренный, следовательно \angle AKD= \angle KDA.
\angle AKD= \angle KDC как накрест лежащие при параллельных AB и CD.Так как \angle AKD= \angle KDA и \angle KDA= \angle KDC, то \angle KDA=\angle KDC.
Источник:
ОГЭ. Математика: типовые экзаменационные варианты: 36 вариантов / под. ред. И.В. Ященко. — М.: Издательство «Национальное образование», 2020. -224 с. -(ОГЭ. ФИПИ — школе).