Тип задания: 16 (Геометрия. Планиметрия).
Id-34. Задание № 16.
Точка O — центр вписанной в треугольник ABC окружности. Прямая BO вторично пересекает описанную около этого треугольника окружность в точке P.
а) Докажите, что \angle POA = \angle PAO
б) Найдите площадь треугольника APO, если радиус описанной около треугольника ABC окружности равен 6, \angle BAC= 75^\circ, \angle ABC=60^\circ
Решение:
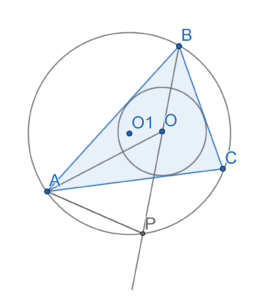
а) Центр вписанной окружности лежит на точке пересечения биссектрис. Следовательно, \angle ABP=\angle PBC и \angle BAO=\angle OAC.
\angle AOB=180^\circ - \angle ABO-\angle OAB \angle POA=180^\circ - \angle AOB= 180^\circ - (180^\circ - \angle ABO-\angle OAB)=\angle ABO+\angle OAB=\angle PAC+\angle OAC \angle PAC=\angle PBC, как вписанные углы, опирающиеся на одну и ту же дугу. \angle PAO=\angle PAC + \angle OAC, по условию.Следовательно, \angle PAO = \angle POA.
б) По условию, \angle ABC=60^\circ. Так, как BP — биссектриса \angle ABC, то \angle ABP=30^\circ.
По теореме синусов, \frac{AP}{sin\angle ABP}=2R, где R — радиус описанной окружности.
Тогда, AP= 2R\cdot {sin\angle ABP}. AP= 2\cdot 6 \cdot sin 30^\circ = 6.
Так как \angle PAO = \angle POA, то треугольник APO — равнобедренный, т.е. AP=PO.
\angle APO = 180-2\cdot \angle AOP = = 180^\circ - 2\cdot (\angle ABP + \angle OAC) = = 180^\circ - 2\cdot \angle ABP - 2\cdot \angle OAC = = 180^\circ - \angle ABC - \angle BAC = = 180^\circ - 60^\circ - 75^\circ = = 45^\circ S_{\triangle APO} = \frac{1}{2}\cdot AP \cdot PO \cdot sin \angle APO = =\frac{1}{2}\cdot 6^2 \cdot sin \angle 45^\circ = = \frac{1}{2}\cdot 36 \cdot \frac{\sqrt{2}}{2} = 9\sqrt{2} .
Источник: ЕГЭ. Математика. Профильный уровень: типовые экзаменационные варианты: 36 вариантов / под. ред. И.В. Ященко. — М.: Издательство «Национальное образование», 2020. -256 с. Вариант 1. Задание 16.