Тип задания:
Геометрия. №24.
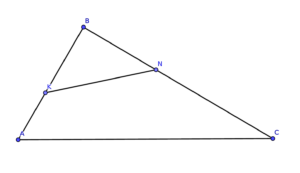
Прямая пересекает стороны AB и BC треугольника ABC в точках K и N соответственно. Известно, что AB=9, BC=12, AC=18, AK=5, CN=9. Найдите длину отрезка KN,
Решение:
KB=AB-AK=9-5=4.
BN=BC-CN=12-9=3.
Заметим, что \frac{AB}{BN}=\frac{9}{3}=\frac{BC}{KB}=\frac{12}{4}=3.
Треугольники ABC и KBN подобны по второму признаку подобия треугольников.
(Угол ABC — общий, \frac{AB}{BN}=\frac{BC}{KB}.)
Следовательно, \frac{AC}{KN}=3.
Тогда KN=\frac{AC}{3}=\frac{18}{3}=6.
Ответ: 6.
Источник:
ОГЭ. Математика: типовые экзаменационные варианты: 36 вариантов / под. ред. И.В. Ященко. — М.: Издательство «Национальное образование», 2020. -224 с. -(ОГЭ. ФИПИ — школе).